算法基础-插入排序&&习题2.1-3、2.1-4

发表于 | 分类于

插入排序

对于少量排序，它是一个很好的算法。开始时，我们的左手为空，并且桌子上的牌面向下。然后，我们每次从桌子上拿走一张牌并将它插入到左手中的正确位置。为了找到一张牌的正确位置，我们从右往左将它与已在手中的每张牌比较。如图所示，拿在左手中的牌总是排序好的。

TypeScript实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class InsertionSort {
    private sortArray: Array<any>

    public constructor(A: Array<any>) {
        this.sortArray = A
        this.insertionSort()
    }

    private insertionSort(): void {
        for (let j = 1; j < this.sortArray.length; j++) {
            let key: any = this.sortArray[j]
            let i: number = j - 1
            
            while (i >= 0 && this.sortArray[i] > key) {
                this.sortArray[i + 1] = this.sortArray[i]
                i = i - 1
            }
            this.sortArray[i + 1] = key
        }
    }

    public printSortResult(): void {
        console.log(this.sortArray)
    }
}

let sort = new InsertionSort([31, 41, 59, 26, 41, 58])
sort.printSortResult()

/* 运算结果：
[ 26, 31, 41, 41, 58, 59 ]
*/

时间复杂度

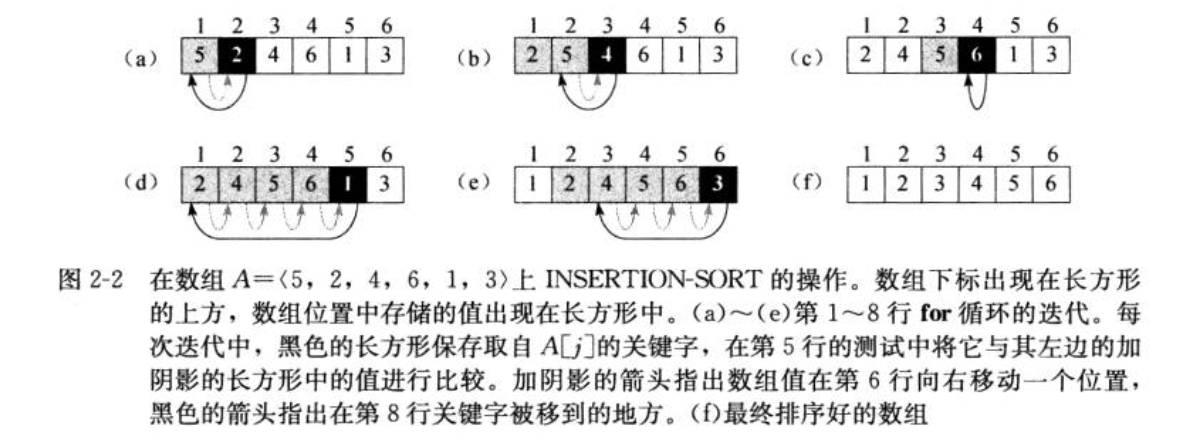
插入排序的时间复杂度分析。在最坏情况下，数组完全逆序，插入第2个元素时要考察前1个元素，插入第3个元素时，要考虑前2个元素，……，插入第N个元素，要考虑前 N - 1 个元素。因此，最坏情况下的比较次数是 1 + 2 + 3 + … + (N - 1)，等差数列求和，结果为 N^2 / 2，所以最坏情况下的复杂度为 O(N^2)。

最好情况下，数组已经是有序的，每插入一个元素，只需要考查前一个元素，因此最好情况下，插入排序的时间复杂度为O(N)。

练习题

考虑以下查找问题：

输入： n个数的一个序列A={ a1, a2, …, an } 和一个值v。
输出： 下标i使得v=A[i]或者当v不在A中时，v为特殊值NIL。
写出线性查找 的伪代码，它扫描整个序列来查找v。使用一个循环不变式来证明你的算法是正确的。确保循环不变式满足三条必要的性质

伪代码

1
2
3
4
5
LINEAR-SEARCH(A, v)
1 for i <- 1 to len(A)
2     do if A[i] == v
3               then return i
4 return NIL

二进制相加

考虑把两个n位二进制证书加起来的问题，这两个整数分别存储在两个n元数组A和B中。这两个整数和应按二进制形式存储在一个（n+1）元数组中。

其实就是二进制相加， 用TypeScript实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class BinaryAddition {
    private A: Array<number> = [1, 1, 0, 0, 1, 0, 1, 1, 1, 0]
    private B: Array<number> = [1, 1, 1, 0, 1, 1, 0, 1, 1, 1]
    private C: Array<number> = []
    private lastflow: number = 0

    public constructor() {
        this.binaryAdditionResult()
        this.printResult()
    }

    private addMethod(a: number, b: number): number {
        let r: number = a + b + this.lastflow
        if (r > 1) {
            this.lastflow = 1
            return r % 2
        } else {
            this.lastflow = 0
            return r
        }
    }

    private binaryAdditionResult(): void {
        let n: number = this.A.length
        for (let i = n - 1; i >= 0; --i) {
            this.C[i + 1] = this.addMethod(this.A[i], this.B[i])
        }
        this.C[0] = this.lastflow
    }

    private printResult(): void {
        console.log('A  ' + this.A)
        console.log('B  ' + this.B)
        console.log('C  ' + this.C)
    }
}

let binaryAddition: BinaryAddition = new BinaryAddition()

/* 运算结果：
A  1,1,0,0,1,0,1,1,1,0
B  1,1,1,0,1,1,0,1,1,1
C  1,1,0,1,1,1,0,0,1,0,1
*/