算法
给出现实生活中需要排序的一个例子或者现实生活中需要计算凸壳的一个例子?
凸包问题
概念
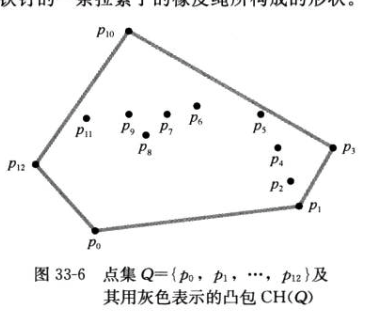
假设平面上有p0~p12共13个点,过某些点作一个多边形,使这个多边形能把所有点都“包”起来。当这个多边形是凸多边形的时候,我们就叫它“凸包”。
直观地讲,可以把Q中每个点都想象成是露在一块板外的铁钉,那么凸包就是包围这些铁钉的一条拉近了的橡皮绳所构成的形状。
实例
根据所有的果树的位置,找出一个n边形的最小篱笆,使 得所有果树都包围在篱笆内部,或者在篱笆边沿上。也就是,一组平面上的点,求一个包含所有点的最小的凸多边形。
除速度外,在真实环境中还可能使用哪些其他有关效率的夺量
占用资源的大小(在计算机中可以成为空间),问题解决的程度
选择一种你以前一直的数据结构,并且讨论其优势和局限
栈:后进先出,非常适合于保存程序调用的迒回地址之类的特殊应用(递归调用),缺点是无法进行随机的读写
最短路径与旅行商问题的相似之处和不同之处
相同之处:都是要求出最短总距离
不同之处:终点的不同,同时最短路径不需要遍历全部的点,而那个旅行商问题就是需要遍历所有的点的问题
商旅问题没有已知的有效算法,然而,我们知道一些算法,他们给朱一个离最小值不太远的总距离。35章中会讨论近似算法问题。
提供一个问题,其中只有最佳解才行,然后提供一个问题,其中近似最佳的一个解也足够好
最短路径、商旅问题
作为技术的一种算法
给出在应用层需要算法内同的应用的一个例子,并且讨论设计的算法的功能
在一次有 210 人参加的考试结束后,老师需要对平均分迕行计算。假设老师不借助于计算机类的自动工具,而是采取传统的手工计算平均分。
计算方法:看过考分后,大概估计一个值K ,然后与 210 个分数的数据迕行比较,找出分数与k的误差ci,如果发现有ci=-ci,则去掉,假设最后的误差和是bi,那么平均分就可以写成K+bi/210.
设计的算法的功能:该算法对于计算机返样的自动化计算工具来说意义不大,但是对于手工
计算来说,却是很实用的。在计算的过程中,首先把大数转换成了小数,然后在比较
时又直接把一些数据剔除,减少了运算量。最终大大加快了计算效率,幵且提高了计
算准确度。
假设我们正在比较插入排序和归并排序在相同机器上面的实现,对于规模为n的输入,插入排序运行8n^2步,而归并排序运行64nlgn步。问对于哪些n值,插入排序优于归并排序?
答: 令 8n^2 < 64nlgn
=> 化简得n < 8lgn
=> 2^(n/8) < 2^(lgn)
=> 2^(n/8) < n
=> 令t=n/8 , n=8t
=> 2^t < 8t
=> 制表:
1 2 3 4 5 6
8t 8 16 24 32 40 48
2^t 2 4 8 16 32 64
当t=0 8t=0 2^t=1
当t=0.2, 8t=1.6 2^t=1.15
当t=5.1, 8t=40.8 2^t=34.3
当t=5.4, 8t=43.2 2^t=42.2
当t=5.5, 8t=44 2^t=45.25
所以,当0.2 < t < 5.5时,即1 < n < 44时,插入排序优于归并。
n的最小值为何值时,运行时间为100n^2的一个算法在相同的机器上面快于运行时间为2^n的另外一个算法
答:令100n^2<2^n =>

由图可得当n>14.325时,满足不等式,又n为正整数,所以n取最小值15。
思考题
运行时间的比较

答:具体的答案数据就不列出来了,但可以肯定的是,从上到下,算法效率是逐渐降低的,意思是说一个算法若能做到lgn的效率是极佳的,而如果做到n!的话则是最不可取的了。